知识拓展练习（经典面试题） / 7. 买卖股票的最佳时机

一、题目

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

二、示例

示例 1：
输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。
示例 2：
输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

三、提示

1 <= prices.length <= 105
0 <= prices[i] <= 104

四、进阶

尽可能想出更多的解决方案，至少有 三种 不同的方法可以解决这个问题。

你可以使用空间复杂度为 O(1) 的 原地 算法解决这个问题吗？

五、参考题解

1、解决方案

我们需要找出给定数组中两个数字之间的最大差值（即，最大利润）。此外，第二个数字（卖出价格）必须大于第一个数字（买入价格）。

形式上，对于每组 i 和 j（其中 j>i）我们需要找出 max⁡(prices[j]−prices[i])。

2、方法一：暴力法

（1）代码

class Solution {
public:
  int maxProfit(vector<int>& prices) {
    int n = (int)prices.size(), ans = 0;
    for (int i = 0; i < n; ++i){
      for (int j = i + 1; j < n; ++j) {
        ans = max(ans, prices[j] - prices[i]);
      }
    }
    return ans;
  }
};


（2）复杂度分析

时间复杂度：O(n^2)。循环运行 n(n−1)/2 次。

空间复杂度：O(1)。只使用了常数个变量。

2、方法二：一次遍历

（1）算法

假设给定的数组为：[7, 1, 5, 3, 6, 4]

如果我们在图表上绘制给定数组中的数字，我们将会得到：

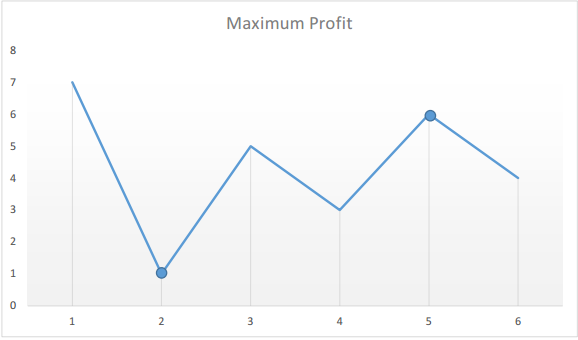
我们来假设自己来购买股票。随着时间的推移，每天我们都可以选择出售股票与否。那么，假设在第 i 天，如果我们要在今天卖股票，那么我们能赚多少钱呢？

显然，如果我们真的在买卖股票，我们肯定会想：如果我是在历史最低点买的股票就好了！太好了，在题目中，我们只要用一个变量记录一个历史最低价格 minprice，我们就可以假设自己的股票是在那天买的。那么我们在第 i 天卖出股票能得到的利润就是 prices[i] - minprice。

因此，我们只需要遍历价格数组一遍，记录历史最低点，然后在每一天考虑这么一个问题：如果我是在历史最低点买进的，那么我今天卖出能赚多少钱？当考虑完所有天数之时，我们就得到了最好的答案。

class Solution {
public:
  int maxProfit(vector<int>& prices) {
    int inf = 1e9;
    int minprice = inf, maxprofit = 0;
    for (int price: prices) {
      maxprofit = max(maxprofit, price - minprice);
      minprice = min(price, minprice);
    }
    return maxprofit;
  }
};


（2）复杂度分析

时间复杂度：O(n)，只需要遍历一次。

空间复杂度：O(1)，只使用了常数个变量。