知识拓展练习（经典面试题） / 50. 插入区间

一、题目

给你一个无重叠的，按照区间起始端点排序的区间列表。

在列表中插入一个新的区间，你需要确保列表中的区间仍然有序且不重叠（如果有必要的话，可以合并区间）。

二、示例

示例 1：

输入：intervals = [[1,3],[6,9]], newInterval = [2,5]
输出：[[1,5],[6,9]]

示例 2：

输入：intervals = [[1,2],[3,5],[6,7],[8,10],[12,16]], newInterval = [4,8]
输出：[[1,2],[3,10],[12,16]]
解释：这是因为新的区间 [4,8] 与 [3,5],[6,7],[8,10] 重叠。

示例 3：

输入：intervals = [], newInterval = [5,7]
输出：[[5,7]]

示例 4：

输入：intervals = [[1,5]], newInterval = [2,3]
输出：[[1,5]]

示例 5：

输入：intervals = [[1,5]], newInterval = [2,7]
输出：[[1,7]]

三、提示

0 <= intervals.length <= 10^4
intervals[i].length == 2
0 <= intervals[i][0] <= intervals[i][1] <= 10^5
intervals 根据 intervals[i][0] 按升序排列
newInterval.length == 2
0 <= newInterval[0] <= newInterval[1] <= 10^5

四、参考题解

1、前言

对于区间 S1=[l1,r1] 和 S2=[l2,r2]，如果它们之间没有重叠（没有交集），说明要么 S1 在 S2 的左侧，此时有 r1<l2；要么 S1 在 S2 的右侧，此时有 l1>r2。

如果 r1<l2 和 l1>r2 二者均不满足，说明 S1 和 S2 必定有交集，它们的交集即为

[max⁡(l1,l2),min⁡(r1,r2)]

并集即为

[min⁡(l1,l2),max⁡(r1,r2)]

2、方法一：模拟

（1）思路与算法

在给定的区间集合 X 互不重叠的前提下，当我们需要插入一个新的区间 S=[left,right] 时，我们只需要：

①找出所有与区间 S 重叠的区间集合 X′；

②将 X′ 中的所有区间连带上区间 S 合并成一个大区间；

③最终的答案即为不与 X′ 重叠的区间以及合并后的大区间。

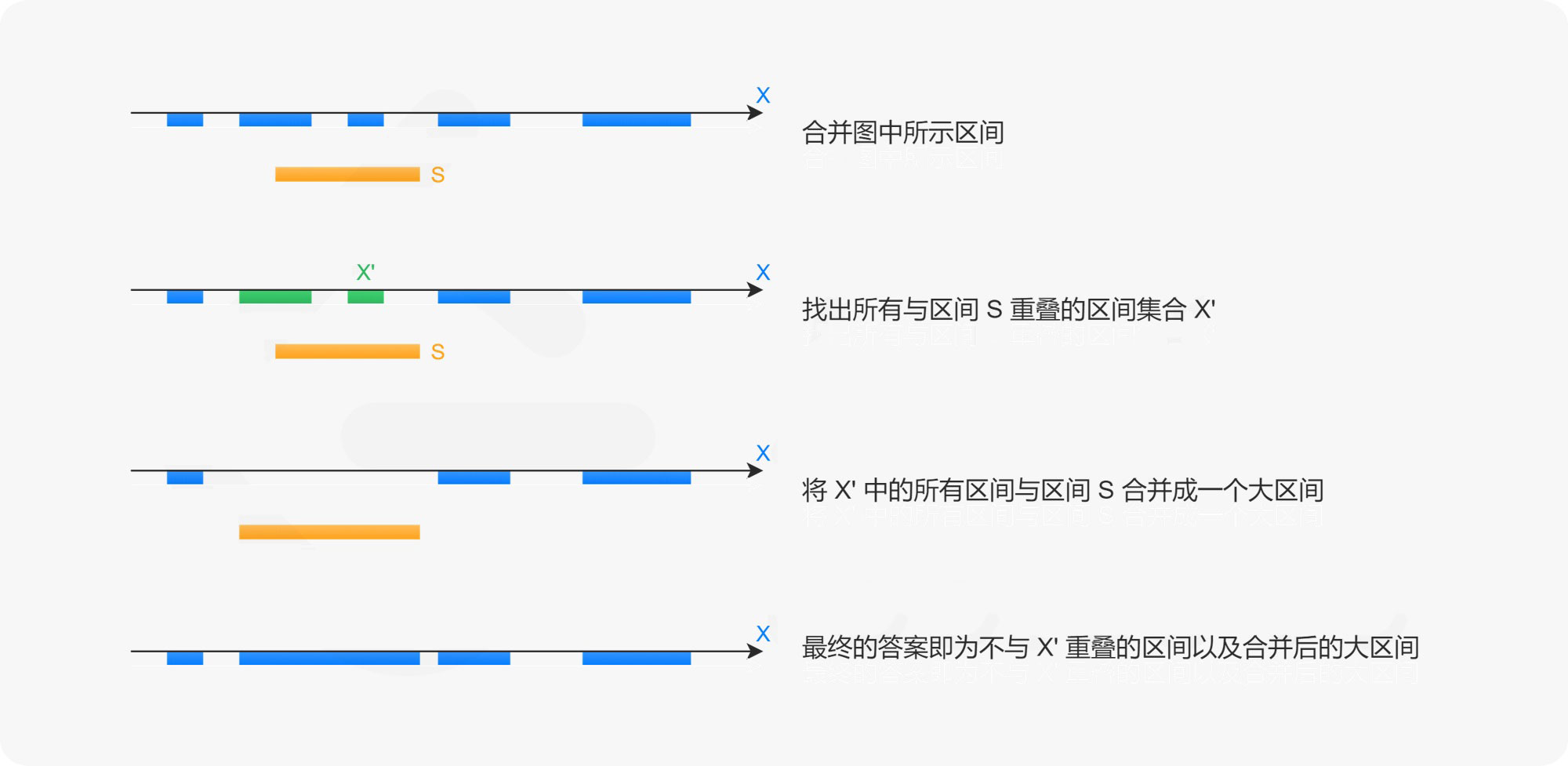
这样做的正确性在于，给定的区间集合中任意两个区间都是没有交集的，因此所有需要合并的区间，就是所有与区间 S 重叠的区间。

并且，在给定的区间集合已经按照左端点排序的前提下，所有与区间 S 重叠的区间在数组 intervals 中下标范围是连续的，因此我们可以对所有的区间进行一次遍历，就可以找到这个连续的下标范围。

当我们遍历到区间 [li,ri] 时：

如果 ri<left，说明 [li,ri] 与 S 不重叠并且在其左侧，我们可以直接将 [li,ri] 加入答案；

如果 li>right，说明 [li,ri] 与 S 不重叠并且在其右侧，我们可以直接将 [li,ri] 加入答案；

如果上面两种情况均不满足，说明 [li,ri] 与 S 重叠，我们无需将 [li,ri] 加入答案。此时，我们需要将 S 与 [li,ri] 合并，即将 S 更新为其与 [li,ri] 的并集。

那么我们应当在什么时候将区间 S 加入答案呢？由于我们需要保证答案也是按照左端点排序的，因此当我们遇到第一个满足 li>right 的区间时，说明以后遍历到的区间不会与 S 重叠，并且它们左端点一定会大于 S 的左端点。此时我们就可以将 S 加入答案。特别地，如果不存在这样的区间，我们需要在遍历结束后，将 S 加入答案。

（2）代码

//Java
class Solution {
  public int[][] insert(int[][] intervals, int[] newInterval) {
    int left = newInterval[0];
    int right = newInterval[1];
    boolean placed = false;
    List<int[]> ansList = new ArrayList<int[]>();
    for (int[] interval : intervals) {
      if (interval[0] > right) {
        // 在插入区间的右侧且无交集
        if (!placed) {
          ansList.add(new int[]{left, right});
          placed = true;
        }
        ansList.add(interval);
      } else if (interval[1] < left) {
        // 在插入区间的左侧且无交集
        ansList.add(interval);
      } else {
        // 与插入区间有交集，计算它们的并集
        left = Math.min(left, interval[0]);
        right = Math.max(right, interval[1]);
      }
    }
    if (!placed) {
      ansList.add(new int[]{left, right});
    }
    int[][] ans = new int[ansList.size()][2];
    for (int i = 0; i < ansList.size(); ++i) {
      ans[i] = ansList.get(i);
    }
    return ans;
  }
}