当前位置：首页 > 知识拓展练习（经典面试题） > 26. 判断子序列

知识拓展练习（经典面试题） / 26. 判断子序列

一、题目

给定字符串 s 和 t ，判断 s 是否为 t 的子序列。

字符串的一个子序列是原始字符串删除一些（也可以不删除）字符而不改变剩余字符相对位置形成的新字符串。（例如，"ace"是"abcde"的一个子序列，而"aec"不是）。

二、示例

示例 1：
输入：s = "abc", t = "ahbgdc"
输出：true
示例 2：
输入：s = "axc", t = "ahbgdc"
输出：false

三、提示

0 <= s.length <= 100
0 <= t.length <= 10^4
两个字符串都只由小写字符组成。

四、进阶

如果有大量输入的 S，称作 S1, S2, ... , Sk 其中 k >= 10亿，你需要依次检查它们是否为 T 的子序列。在这种情况下，你会怎样改变代码？

五、参考题解

1、方法一：双指针

（1）思路及算法

本题询问的是，s 是否是 t 的子序列，因此只要能找到任意一种 s 在 t 中出现的方式，即可认为 s 是 t 的子序列。

而当我们从前往后匹配，可以发现每次贪心地匹配靠前的字符是最优决策。

假定当前需要匹配字符 c，而字符 c 在 t 中的位置 x1 和 x2 出现（x1<x2），那么贪心取 x1 是最优解，因为 x2 后面能取到的字符，x1 也都能取到，并且通过 x1 与 x2 之间的可选字符，更有希望能匹配成功。

这样，我们初始化两个指针 i 和 j，分别指向 s 和 t 的初始位置。每次贪心地匹配，匹配成功则 i 和 j 同时右移，匹配 s 的下一个位置，匹配失败则 j 右移，i 不变，尝试用 t 的下一个字符匹配 s。

最终如果 i 移动到 s 的末尾，就说明 s 是 t 的子序列。

class Solution {
  public boolean isSubsequence(String s, String t) {
    int n = s.length(), m = t.length();
    int i = 0, j = 0;
    while (i < n && j < m) {
      if (s.charAt(i) == t.charAt(j)) {
        i++;
      }
      j++;
    }
    return i == n;
  }
}

（2）复杂度分析

时间复杂度：O(n+m)，其中 n 为 s 的长度，m 为 t 的长度。每次无论是匹配成功还是失败，都有至少一个指针发生右移，两指针能够位移的总距离为 n+m。

空间复杂度：O(1)。

2、方法二：动态规划

（1）思路及算法

考虑前面的双指针的做法，我们注意到我们有大量的时间用于在 t 中找到下一个匹配字符。

这样我们可以预处理出对于 t 的每一个位置，从该位置开始往后每一个字符第一次出现的位置。

我们可以使用动态规划的方法实现预处理，令 f[i][j] 表示字符串 t 中从位置 i 开始往后字符 j 第一次出现的位置。在进行状态转移时，如果 t 中位置 i 的字符就是 j，那么 f[i][j]=i，否则 j 出现在位置 i+1 开始往后，即 f[i][j]=f[i+1][j]，因此我们要倒过来进行动态规划，从后往前枚举 i。

这样我们可以写出状态转移方程：

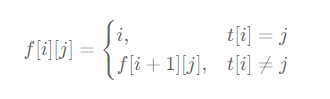
假定下标从 0 开始，那么 f[i][j] 中有 0≤i≤m−1，对于边界状态 f[m−1][..]，我们置 f[m][..] 为 m，让 f[m−1][..] 正常进行转移。这样如果 f[i][j]=m，则表示从位置 i 开始往后不存在字符 j。

这样，我们可以利用 f 数组，每次 O(1) 地跳转到下一个位置，直到位置变为 m 或 s 中的每一个字符都匹配成功。

同时我们注意到，该解法中对 t 的处理与 s 无关，且预处理完成后，可以利用预处理数组的信息，线性地算出任意一个字符串 s 是否为 t 的子串。这样我们就可以解决「后续挑战」啦。

（2）代码

//Java
class Solution {
  public boolean isSubsequence(String s, String t) {
    int n = s.length(), m = t.length();
    int[][] f = new int[m + 1][26];
    for (int i = 0; i < 26; i++) {
      f[m][i] = m;
    }
    for (int i = m - 1; i >= 0; i--) {
      for (int j = 0; j < 26; j++) {
        if (t.charAt(i) == j + 'a')
          f[i][j] = i;
        else
          f[i][j] = f[i + 1][j];
      }
    }
    int add = 0;
    for (int i = 0; i < n; i++) {
      if (f[add][s.charAt(i) - 'a'] == m) {
        return false;
      }
      add = f[add][s.charAt(i) - 'a'] + 1;
    }
    return true;
  }
}