知识拓展练习（经典面试题） / 18. 整数转罗马数字

一、题目

罗马数字包含以下七种字符： I， V， X， L，C，D 和 M。

字符	数值
I	1
V	5
X	10
L	50
C	100
D	500
M	1000

例如，罗马数字 2 写做 II ，即为两个并列的 1。12 写做 XII ，即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。

通常情况下，罗马数字中小的数字在大的数字的右边。但也存在特例，例如 4 不写做 IIII，而是 IV。数字 1 在数字 5 的左边，所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地，数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况：

I 可以放在 V (5) 和 X (10) 的左边，来表示 4 和 9。

X 可以放在 L (50) 和 C (100) 的左边，来表示 40 和 90。

C 可以放在 D (500) 和 M (1000) 的左边，来表示 400 和 900。

给你一个整数，将其转为罗马数字。

二、示例

示例 1:
输入: num = 3
输出: "III"
示例 2:
输入: num = 4
输出: "IV"
示例 3:
输入: num = 9
输出: "IX"
示例 4:
输入: num = 58
输出: "LVIII"
解释: L = 50, V = 5, III = 3.
示例 5:
输入: num = 1994
输出: "MCMXCIV"
解释: M = 1000, CM = 900, XC = 90, IV = 4.

三、提示

1 <= num <= 3999

四、参考题解

1、前言

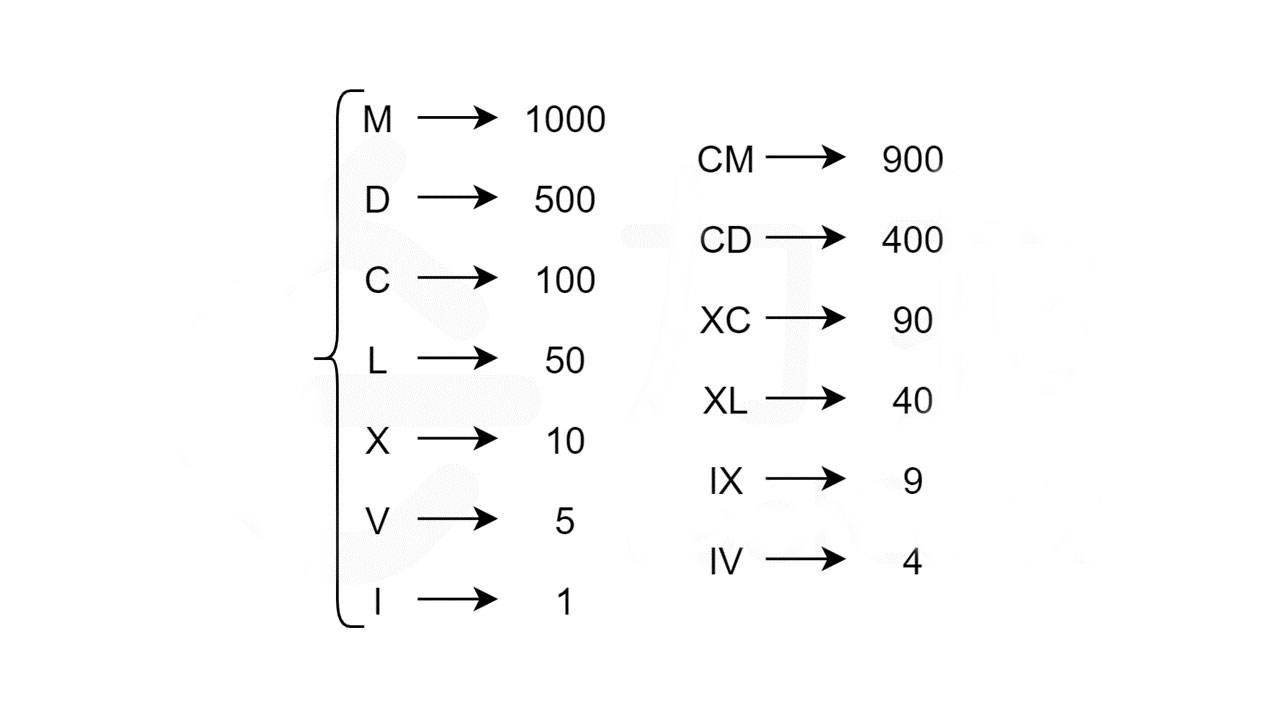
（1）罗马数字符号

罗马数字由 7 个不同的单字母符号组成，每个符号对应一个具体的数值。此外，减法规则（如问题描述中所述）给出了额外的 6 个复合符号。这给了我们总共 13 个独特的符号（每个符号由 1 个或 2 个字母组成），如下图所示。

（2）罗马数字的唯一表示法

让我们从一个例子入手。考虑 140 的罗马数字表示，下面哪一个是正确的？

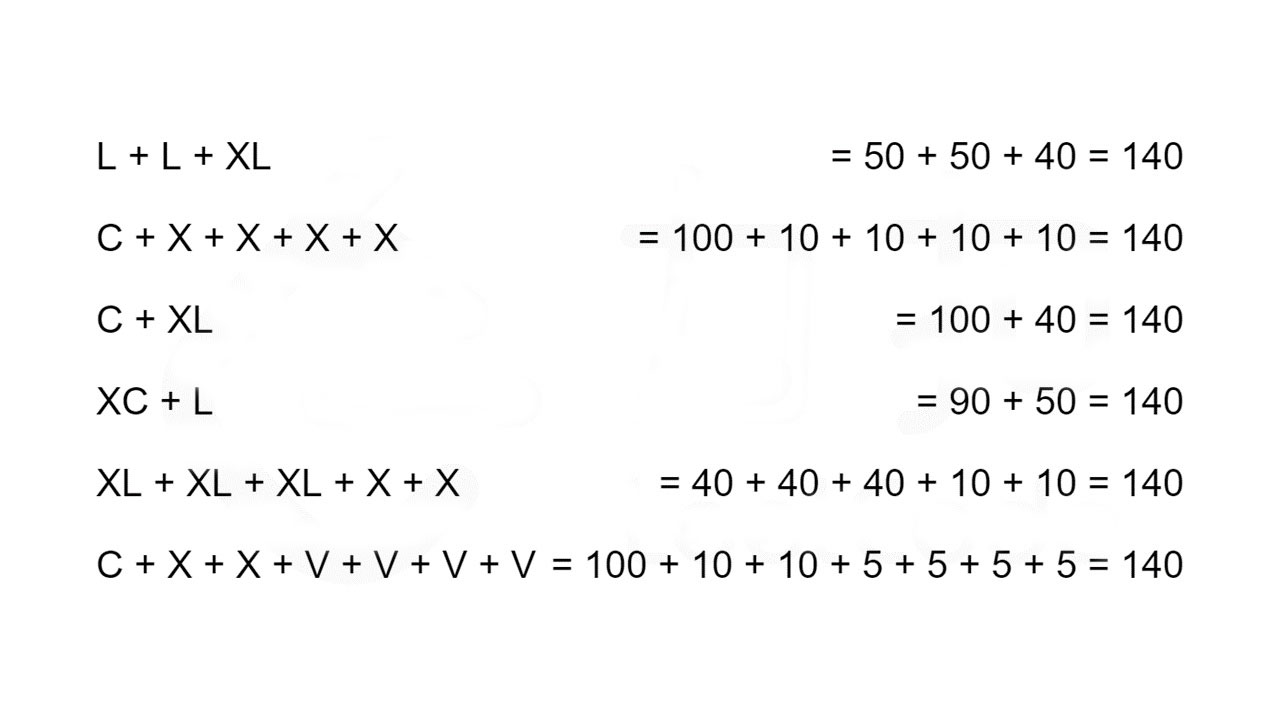
我们用来确定罗马数字的规则是：对于罗马数字从左到右的每一位，选择尽可能大的符号值。对于 140，最大可以选择的符号值为 C=100。接下来，对于剩余的数字 40，最大可以选择的符号值为 XL=40。因此，140 的对应的罗马数字为 C+XL=CXL。

2、方法一：模拟

（1）思路

根据罗马数字的唯一表示法，为了表示一个给定的整数 num，我们寻找不超过 num 的最大符号值，将 num 减去该符号值，然后继续寻找不超过 num 的最大符号值，将该符号拼接在上一个找到的符号之后，循环直至 num 为 0。最后得到的字符串即为 num 的罗马数字表示。

编程时，可以建立一个数值-符号对的列表 valueSymbols，按数值从大到小排列。遍历 valueSymbols 中的每个数值-符号对，若当前数值 value 不超过 num，则从 num 中不断减去 value，直至 num 小于 value，然后遍历下一个数值-符号对。若遍历中 num 为 0 则跳出循环。

（2）代码

//Java
class Solution {
  int[] values = {1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1};
  String[] symbols = {"M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"};
  public String intToRoman(int num) {
    StringBuffer roman = new StringBuffer();
    for (int i = 0; i < values.length; ++i) {
      int value = values[i];
      String symbol = symbols[i];
      while (num >= value) {
        num -= value;
        roman.append(symbol);
      }
      if (num == 0) {
        break;
      }
    }
    return roman.toString();
  }
}

（3）复杂度分析

时间复杂度：O(1)。由于 valueSymbols 长度是固定的，且这 13 字符中的每个字符的出现次数均不会超过 3，因此循环次数有一个确定的上限。对于本题给出的数据范围，循环次数不会超过 15 次。

空间复杂度：O(1)。

3、方法二：硬编码数字

（1）思路

回顾前言中列出的这 13 个符号，可以发现：

千位数字只能由 M 表示；

百位数字只能由 C，CD，D 和 CM 表示；

十位数字只能由 X，XL，L 和 XC 表示；

个位数字只能由 I，IV，V 和 IX 表示。

这恰好把这 13 个符号分为四组，且组与组之间没有公共的符号。因此，整数 num 的十进制表示中的每一个数字都是可以单独处理的。

进一步地，我们可以计算出每个数字在每个位上的表示形式，整理成一张硬编码表。如下图所示，其中 0 对应的是空字符串。

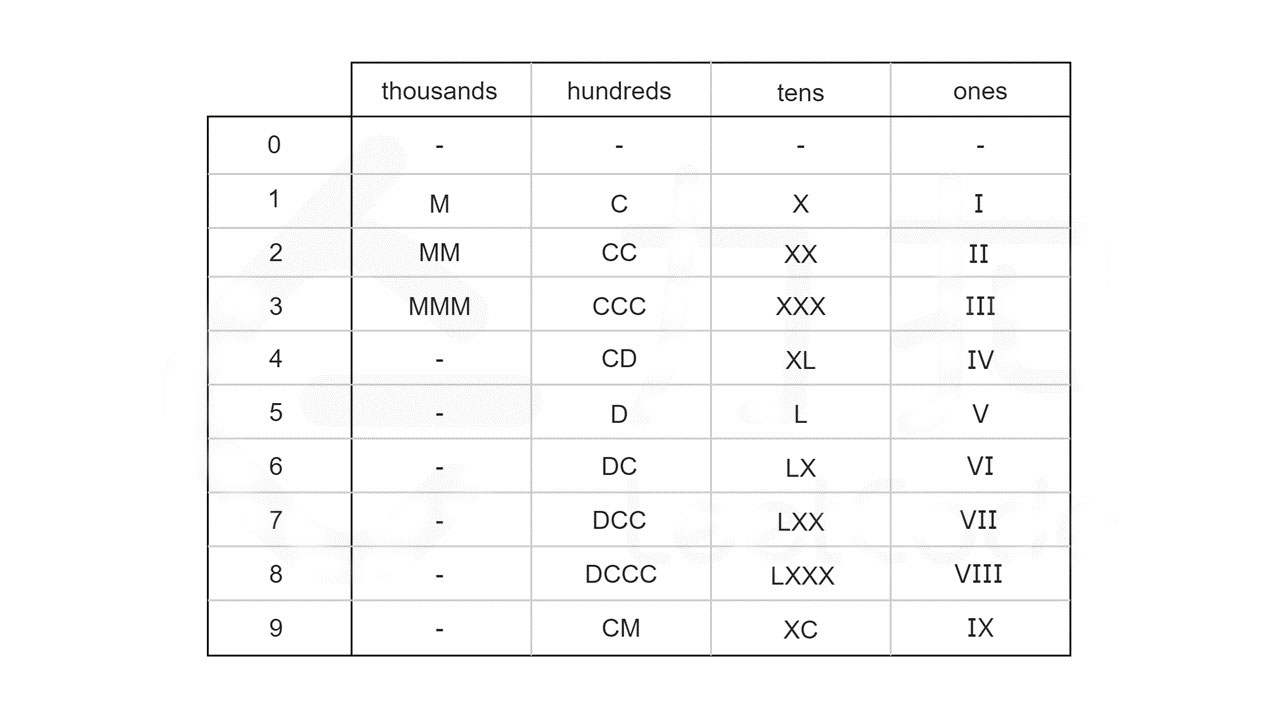
利用模运算和除法运算，我们可以得到 num 每个位上的数字：

thousands_digit = num / 1000
hundreds_digit = (num % 1000) / 100
tens_digit = (num % 100) / 10
ones_digit = num % 10

最后，根据 num 每个位上的数字，在硬编码表中查找对应的罗马字符，并将结果拼接在一起，即为 num 对应的罗马数字。

（2）代码

class Solution {
  String[] thousands = {"", "M", "MM", "MMM"};
  String[] hundreds = {"", "C", "CC", "CCC", "CD", "D", "DC", "DCC", "DCCC", "CM"};
  String[] tens   = {"", "X", "XX", "XXX", "XL", "L", "LX", "LXX", "LXXX", "XC"};
  String[] ones   = {"", "I", "II", "III", "IV", "V", "VI", "VII", "VIII", "IX"};
  public String intToRoman(int num) {
    StringBuffer roman = new StringBuffer();
    roman.append(thousands[num / 1000]);
    roman.append(hundreds[num % 1000 / 100]);
    roman.append(tens[num % 100 / 10]);
    roman.append(ones[num % 10]);
    return roman.toString();
  }
}

（3）复杂度分析

时间复杂度：O(1)。计算量与输入数字的大小无关。

空间复杂度：O(1)。