知识拓展练习(经典面试题) / 10. 跳跃游戏 II
一、题目
给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。
每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说,如果你在 nums[i] 处,你可以跳转到任意 nums[i + j] 处:
① 0 <= j <= nums[i]
② i + j < n
返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。
二、示例
示例 1:
输入: nums = [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
示例 2:
输入: nums = [2,3,0,1,4]
输出: 2
三、提示
1 <= nums.length <= 10^4
0 <= nums[i] <= 1000
题目保证可以到达 nums[n-1]
四、参考题解
1、解题思路
这道题是典型的贪心算法,通过局部最优解得到全局最优解。以下两种方法都是使用贪心算法实现,只是贪心的策略不同。
2、方法一:反向查找出发位置
我们的目标是到达数组的最后一个位置,因此我们可以考虑最后一步跳跃前所在的位置,该位置通过跳跃能够到达最后一个位置。
如果有多个位置通过跳跃都能够到达最后一个位置,那么我们应该如何进行选择呢?直观上来看,我们可以「贪心」地选择距离最后一个位置最远的那个位置,也就是对应下标最小的那个位置。因此,我们可以从左到右遍历数组,选择第一个满足要求的位置。
找到最后一步跳跃前所在的位置之后,我们继续贪心地寻找倒数第二步跳跃前所在的位置,以此类推,直到找到数组的开始位置。
使用这种方法编写的 C++ 和 Python 代码会超出时间限制,因此我们只给出 Java 和 Go 代码。
//Java
class Solution {
public int jump(int[] nums) {
int position = nums.length - 1;
int steps = 0;
while (position > 0) {
for (int i = 0; i < position; i++) {
if (i + nums[i] >= position) {
position = i;
steps++;
break;
}
}
}
return steps;
}
}
复杂度分析
时间复杂度:O(n^2),其中 n 是数组长度。有两层嵌套循环,在最坏的情况下,例如数组中的所有元素都是 1,position 需要遍历数组中的每个位置,对于 position 的每个值都有一次循环。
空间复杂度:O(1)。
3、方法二:正向查找可到达的最大位置
方法一虽然直观,但是时间复杂度比较高,有没有办法降低时间复杂度呢?
如果我们「贪心」地进行正向查找,每次找到可到达的最远位置,就可以在线性时间内得到最少的跳跃次数。
例如,对于数组 [2,3,1,2,4,2,3],初始位置是下标 0,从下标 0 出发,最远可到达下标 2。下标 0 可到达的位置中,下标 1 的值是 3,从下标 1 出发可以达到更远的位置,因此第一步到达下标 1。
从下标 1 出发,最远可到达下标 4。下标 1 可到达的位置中,下标 4 的值是 4 ,从下标 4 出发可以达到更远的位置,因此第二步到达下标 4。
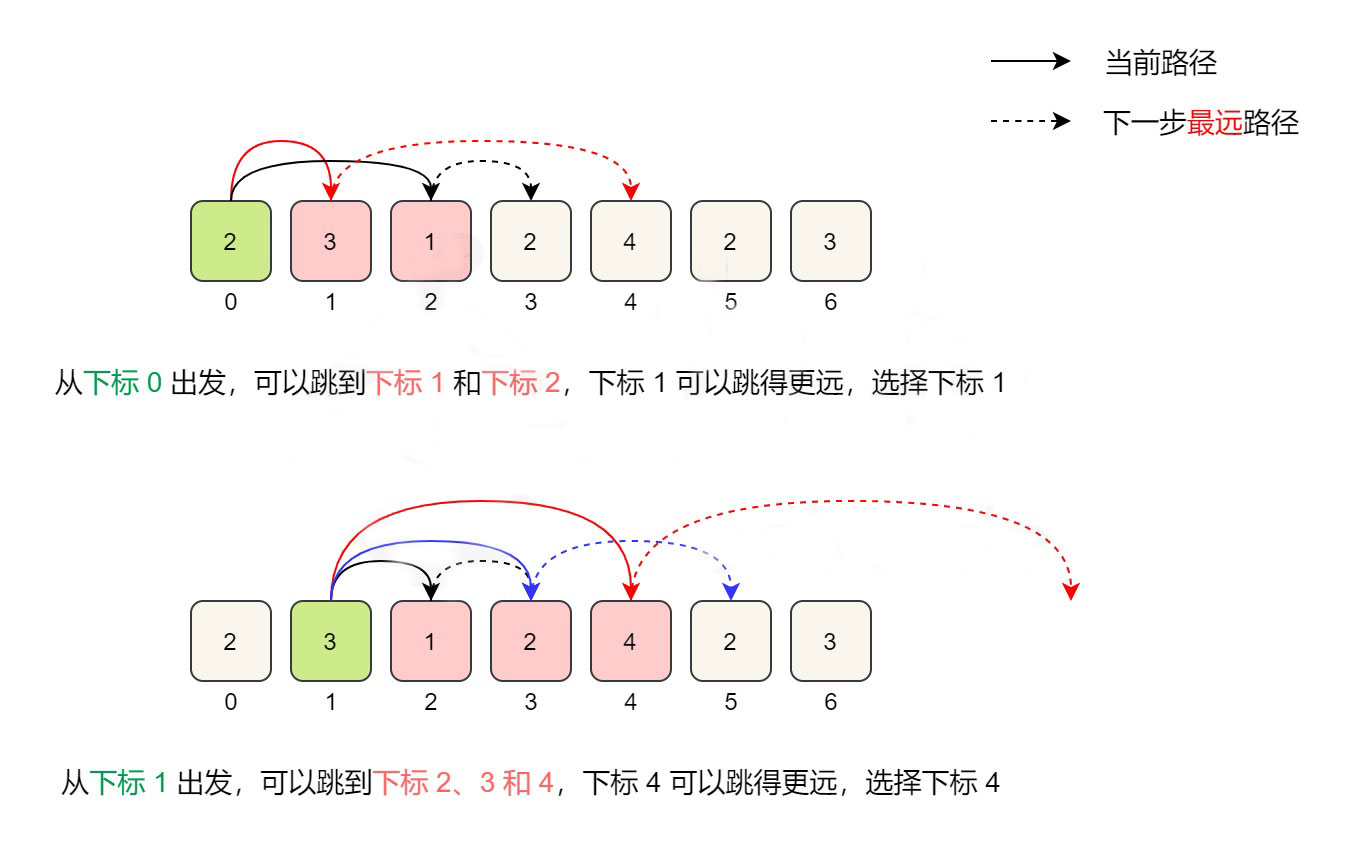
在具体的实现中,我们维护当前能够到达的最大下标位置,记为边界。我们从左到右遍历数组,到达边界时,更新边界并将跳跃次数增加 1。
在遍历数组时,我们不访问最后一个元素,这是因为在访问最后一个元素之前,我们的边界一定大于等于最后一个位置,否则就无法跳到最后一个位置了。如果访问最后一个元素,在边界正好为最后一个位置的情况下,我们会增加一次「不必要的跳跃次数」,因此我们不必访问最后一个元素。
class Solution {
public:
int jump(vector<int>& nums) {
int maxPos = 0, n = nums.size(), end = 0, step = 0;
for (int i = 0; i < n - 1; ++i) {
if (maxPos >= i) {
maxPos = max(maxPos, i + nums[i]);
if (i == end) {
end = maxPos;
++step;
}
}
}
return step;
}
};
复杂度分析
时间复杂度:O(n),其中 n 是数组长度。
空间复杂度:O(1)。
